
6月11日,谷歌量子人工智能团队在arxiv上发表77页长文,通过高阶超前序关联函数体现量子计算机在高灵敏度和高复杂度量子动力学探测中的优越性。

量子可观测值是表征量子多体系统动力学的关键。然而,在具有高纠缠生成动力学的系统中,量子观测值通常会对底层动力学的细节变得不敏感,这使得传统的观测方法在长时间尺度上难以有效工作。目前已经实现在实验中利用重复时间反转协议来恢复量子观测值的敏感性。但在强纠缠动力学中,这些方法的敏感性会显著下降。为了解决在量子多体系统中表征和分析动力学的问题,这篇文章通过二阶超前序关联函数(OTOC(2),out-of-time-order correlators)来探测量子混沌和信息扰乱现象。
OTOC(k)的定义如下:
C(2k)= ⟨Uk†(t)MUk(t)M⟩=⟨(B(t)M)2k⟩
U是多体单元,⟨…⟩表示对特定初始态的期望值。
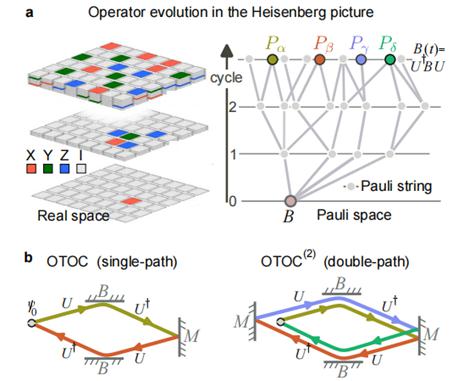
▲OTOC的构造
为了理解重复时间反转如何恢复对量子动力学的敏感性,研究者考虑了测量Pauli算子M的情况。测量值在时间t时等价于时间有序关联函数(TOC,time-ordered correlator),即⟨M(t)M⟩,其中M(t)=U†(t)MU(t)表示在Heisenberg图景中演化后的M。 B(t)=U†(t)BU(t) 是另一个Pauli算子B作用于距离qm一定距离的量子比特qb的时间演化.
实验使用了103个量子比特的超导量子处理器来遍历表征动力学。实验量子电路由随机单比特门和固定的双比特门组成。通过改变单比特门的随机参数来生成不同的电路实例。对于固定的电路周期t,重复测量C (2k)(t, qm, qb, i) 直到测量的统计噪声小于其平均值的10%,然后通过改变t, qm和qb以及电路实例(被采样50到250次)来重复该协议。所有实验的C(4)或C (2)值都通过误差缓解策略进行全局重新缩放。
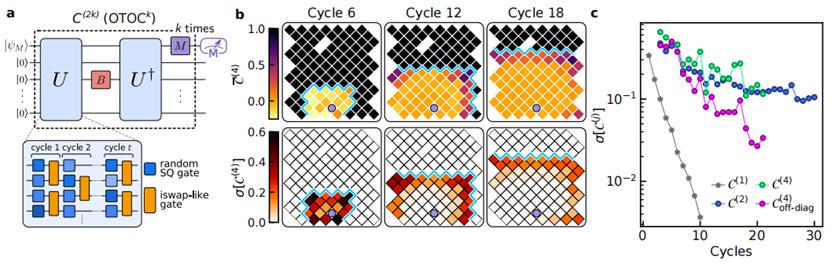
▲OTOC的敏感性
通过测量不同电路周期下的C(4)值,发现它的标准偏差在t=20之后仍然大于0.01。然而TOC的标准偏差(不具有OTOC的回声状结构)随时间呈指数衰减,在t=9时变为<0.01,表明OTOC(2)对量子动力学具有较高的敏感性。
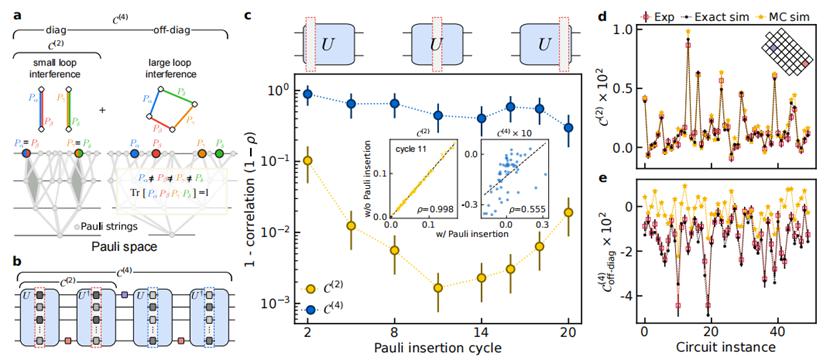
▲OTOC的量子干涉和经典仿真复杂性
插入随机Pauli算子显著改变了OTOC(2)的值,表明OTOC(2)主要由Pauli字符串之间的大环干涉主导。
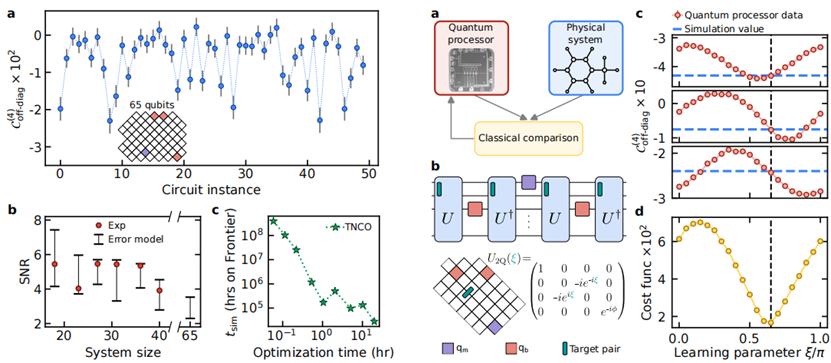
▲OTOC的量子动力学模拟优越性
观察到的干涉机制赋予了OTOC(2)较高的模拟复杂度,在达到相同精度的情况下,在传统的超级计算机上的张量网络收缩需要约3.2年,比起OTOC(2)量子动力学模拟的2.1小时,时间高出13000倍,表明OTOC的量子动力学模拟的优越性。在一维哈密顿量学习的尝试中,物理系统提供了一组OTOC(2)数据,并将其与特定值的量子模拟进行比较,然后优化未知参数,直到量子模拟数据与真实世界的实验数据相匹配,结果显示系统模拟出的未知量在目标值附近,损失函数在目标值处收敛,体现了其在物理系统中的实际应用。
总的来说,本文通过实验验证了高阶OTOC(2)在探测量子动力学中的有效性,并展示了其在经典模拟中的高复杂度。研究结果表明,OTOC(2)是一种可行的实现量子优势的途径,特别是在需要高灵敏度和高经典模拟复杂度的实际应用中。未来可以进一步探索OTOC(2)在复杂的哈密顿量学习等实际任务中的应用潜力。

本文的研究者除了来自谷歌量子人工智能团队,还有很多来自知名顶尖学术机构。
编译:youyou
原文链接:https://arxiv.org/html/2506.10191v1#:~:text=In%20our%20work%2C%20we%20perform%20a%20family%20of,inaccessible%20without%20time%20reversal%20or%20via%20numerical%20methods.














